前言
虽然前端面试中很少会考到算法类的题目,但是你去大厂面试的时候就知道了,对基本算法的掌握对于从事计算机科学技术的我们来说,还是必不可少的,每天花上 10 分钟,了解一下基本算法概念以及前端的实现方式。
另外,掌握了一些基本的算法实现,对于我们日常开发来说,也是如虎添翼,能让我们的 js 业务逻辑更趋高效和流畅。
冒泡排序算法介绍
冒泡排序很简单,就是数组中的相邻元素,两两比较,数值或者 Unicode 码小的元素往前排。
具体实现指导如下:
- 比较相邻两个元素,若前一个比后一个大,则交换位置;
- 第一轮结束之后,最后一个元素的值是最大的;
- 接着开始第二轮,但是不用再比较最后一个元素了;
- 第一轮除外,以后的每一轮都比前一轮少比较一次;

冒泡排序具体实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
var bubbleSort = function (arr){ var i, j, m; var len = arr.length; if (len <= 1) { return arr; } for (i=0; i<len-1; i ) { for (j=0; j<len-i-1; j ) { if (arr[j] > arr[j-1]) { m = arr[j]; arr[j] = arr[j-1]; arr[j-1] = m; } } } return arr; }; |
算法改进
如果数组原本的顺序就是冒泡的,又或者仅做完前面寥寥几次就已经达到效果了,那后续的比较工作就显得有些多余了,如何对以上算法进行改进?
我们可以在某一轮的循环比较结束后,如果没有发生任何的元素交换,则可以认为该数组已经达到预期效果,不必再继续下一轮的比较了。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
var bubbleSort = function (arr){ var start = new Date(); var i, j, m, noswap=true; var len = arr.length; if (len <= 1) { return arr; } for (i=0; i<len-1; i++) { for (j=0; j<len-i-1; j++) { if (arr[j] > arr[j-1]) { m = arr[j]; arr[j] = arr[j-1]; arr[j-1] = m; noswap = false; } } if (noswap) { break; } } // 当 arr 的长度越长,时间差越明显 console.log( new Date() - start); return arr; }; |
时间度复杂度分析
分析时间复杂度就按最坏的情况来,即待排序表是完全逆序的情况。 假设数组中共有 n 个元素,第一轮需要比较 n-1 次,第二轮需要比较 n-2 次,第三轮需要比较 n-3 次,以此类推,最后一轮需要比较 1 次,共比较 n-1 轮,所以是个等差数列,运用等差数列求和公式,能计算出如下时间复杂度: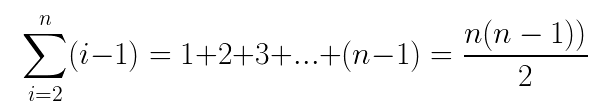
因此总的时间复杂度为 O(n²)。
简单选择排序 算法介绍
打个比方,喜欢短线炒股的朋友,习惯短时间内不断地买进卖出,通过价差来实现盈利。但是通常如此频繁操作,即使失误不多,也会因为操作的手续费和印花税而获利较少。另外一种长线炒股的朋友,习惯长时间持有,不断地观察和判断,时机一到便果断买进或卖出,交易次数少,收益颇丰。
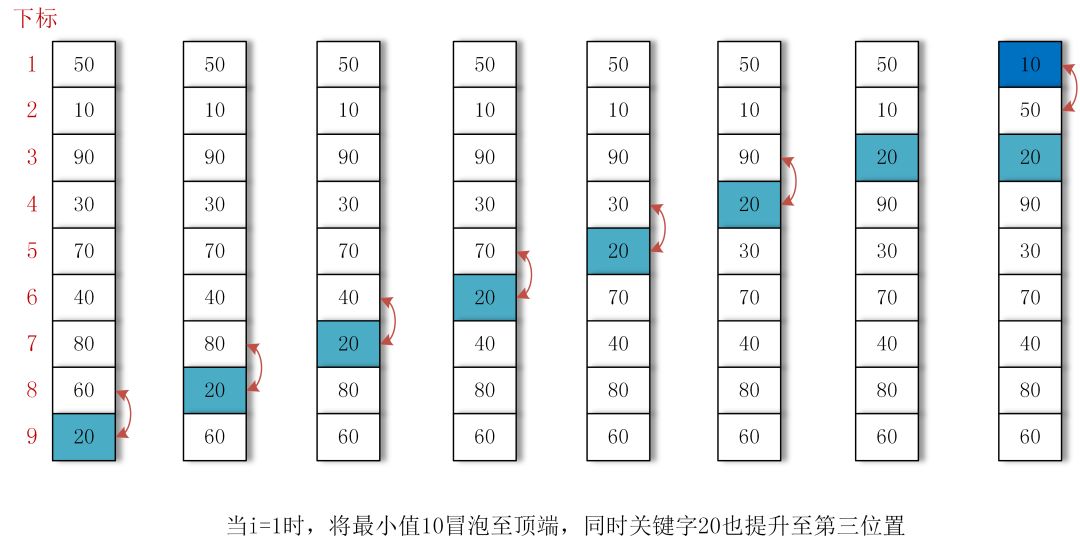
上一节说的冒泡排序就类似于短线炒股,不断地比较之后进行交换,完成排序。而本节所要讲解的简单选择排序,类似于长线炒股,虽然也在不断地观察比较,但是会在合适的时机进行交换,并且只移动一次就完成相应关键字的排序定位工作。这就是选择排序法的初步思想。
算法图示:
具体实现指导: 假设数组中元素个数为 n,则需要比较 n-1 轮,在第 i(1<=i<=n) 轮时,需要经过 n-i 1 次比较,选出 Unicode 码最小的元素,并在本轮结束后与第 i 个元素进行交换,当然了,若第 i 个元素本来就是最小的,就不用进行交换了。注:约定第 1 个元素的下标为 0。
简单选择排序具体实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
var swap = function(arr, posl, posr){ var m = arr[posl]; arr[posl] = arr[posr]; arr[posr] = m; }; var simpleSelect = function(arr){ var len = arr.length; var i, j, min; for (i=0; i<len-1; i++) { min = i; for (j=i 1; j<len; j++) { if (arr[min] > arr[j]) { // 两两比较,将 Unicode 值更小的元素的下标保存到变量 min 中 min = j; } } // 交换元素提取到此处,则交换次数将比冒泡排序的少 if (min !== i) { swap(arr, i, min); } } return arr; }; |
复杂度分析
从以上过程来看,简单选择排序的最大特点就是交换元素的次数相当少,节约了相应的时间。当然数据量越大的时候,节约的时间约明显。
分析其时间复杂度发现,无论最好还是最坏的情况,其与冒泡排序的比较次数都是一样的,最坏情况下,时间复杂度如下: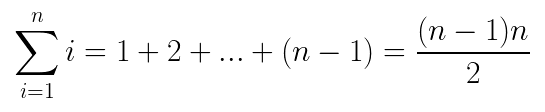
但是对于交换次数而言,当最好的情况下,交换次数为 0,与冒泡排序的相同;最差的情况下,交换次数为 n-1次,比冒泡排序的 n(n-1)/2 次少了一个数量级。基于比较和交换次数的综合,可以得知,简单选择排序的时间复杂度依然为 O(n²)。
尽管简单选择排序与冒泡排序的时间复杂度同为 O(n²),但简单选择排序在性能上还是略优于冒泡排序的。
直接插入排序 算法介绍
我们都应该玩过扑克牌了,游戏期间玩家们基本上都是一边摸牌一边理牌,会把牌面值小的牌放到左边,牌面值大的牌放到右边,以升序进行排序(当然也有喜欢降序排序的玩家)。而理牌期间,我们习惯从左往右看牌面值大小,两两比较,将牌抽出,插入到合理的位置。这里我们理牌的方法,就是「直接插入排序法」。
直接插入排序法的基本操作是将一个元素插入到已经排好序的数组中,从而得到一个新的、 Unicode 值递增的数组。
算法图示:
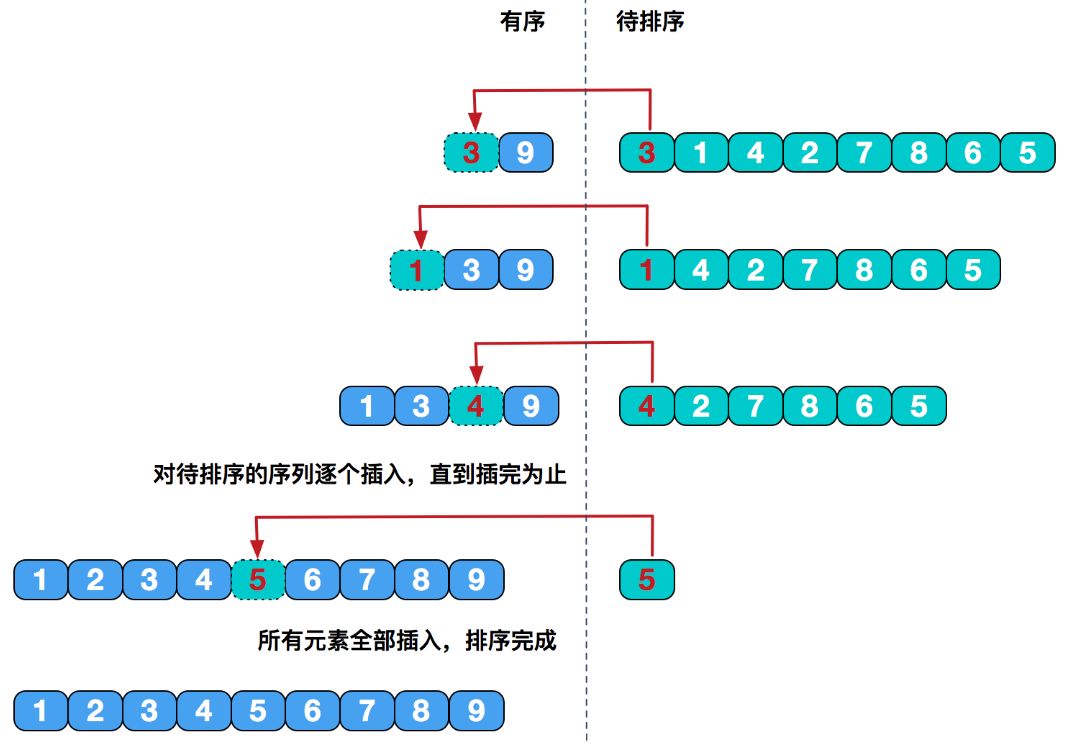
具体实现指导:
假设数组 arr 中共有 n 个元素,因为比较的话,起码要两个元素,则将要进行 n-1 轮循环。每一轮循环比较下标为 i-1、i(1 <= i <= arr.length-1) 的元素,如果后者元素 Unicode 值更大,则将后者元素先保存到一个变量中,并称该变量为「哨兵变量」。然后进入子循环。从下标为 i-1 的元素开始,每一轮子循环中,都去比较当前元素与「哨兵变量」的 Unicode 值,若当前元素更大,则直接将当前元素的值赋给后一个元素(下标加 1 的元素),然后继续下一轮子循环,直到当前元素不大于「哨兵变量」,则退出子循环,继而进行下一轮的循环。

直接插入排序具体实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
function insertSort2(arr) { // m记录最小元素值 var i, j, m, mCnt = 0; var len = arr.length; for (i = 1; i < len; i++) { // 数组前一个值大时 if (arr[i] < arr[i - 1]) { // 将更小的那个元素保存起来 m = arr[i]; // 循环向上判断,当前值大于最小值时 for (j = i - 1; arr[j] > m; j--) { // 往后挪 arr[j + 1] = arr[j]; // mCnt++; } // console.log('移动了' + mCnt + ' 次'); // mCnt = 0; // 直接插入 arr[j+1] = m; } } // console.log(arr) return arr; }; |
复杂度分析
当最好的情况,也就是传入的数组本来就是有序的,比如 [1,2,3,4,5],那么比较次数为 5-1=4 次,由于已经是有序的了,因此没有移动的次数,时间复杂度为 O(n)。
当最坏的情况,也就是传入的数组完全是逆序的,比如 [5,4,3,2,1],那么需要比较如下次: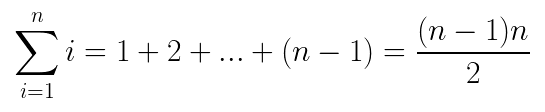
而移动的次数也将达到如下次数: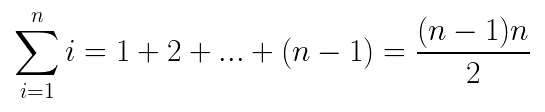
综上所述,时间复杂度依旧为 O(n²)。
希尔排序算法介绍
希尔排序,也称递减增量排序算法,是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。——维基百科
希尔排序是 D.L.Shell 于 1959 年提出来的一种排序算法,在这之前排序算法的时间复杂度基本都是 O(n²),希尔排序算法是突破该事件复杂度的第一批算法之一。
科学家希尔研究出来的这种排序方法,对直接插入排序改进后可以增加效率。
希尔排序算法阐释
上一节我们讲到的「直接插入排序」,它的效率在数组本身就是基本有序以及元素个数较少时,它的效率是很高的。但问题就是,这两个条件本身就很苛刻。如何让程序争取实现这俩条件呢?答案就是将原本有大量元素的数组进行分组,分隔成若干子数组,这样每个子数组的待排序的元素个数就比较少了,然后在子数组内分别进行「直接插入排序」,当整个数组基本有序时,再对全体元素进行一次「直接插入排序」。
所谓基本有序,就是小的元素基本在前面,大的基本在后面,不大不小的基本在中间。要注意像 [2,1,3,6,4,7,5,8,9] 这样的可以称为基本有序,但 [1,5,9,3,7,8,2,4,6] 这样的就谈不上了。
因此我们在分割子数组时,需要采取跳跃分割的策略:将相距某个增量的记录组成一个子数组,这样才能保证在子数组内分别进行直接插入排序后的得到的结果是基本有序,而不是局部有序。
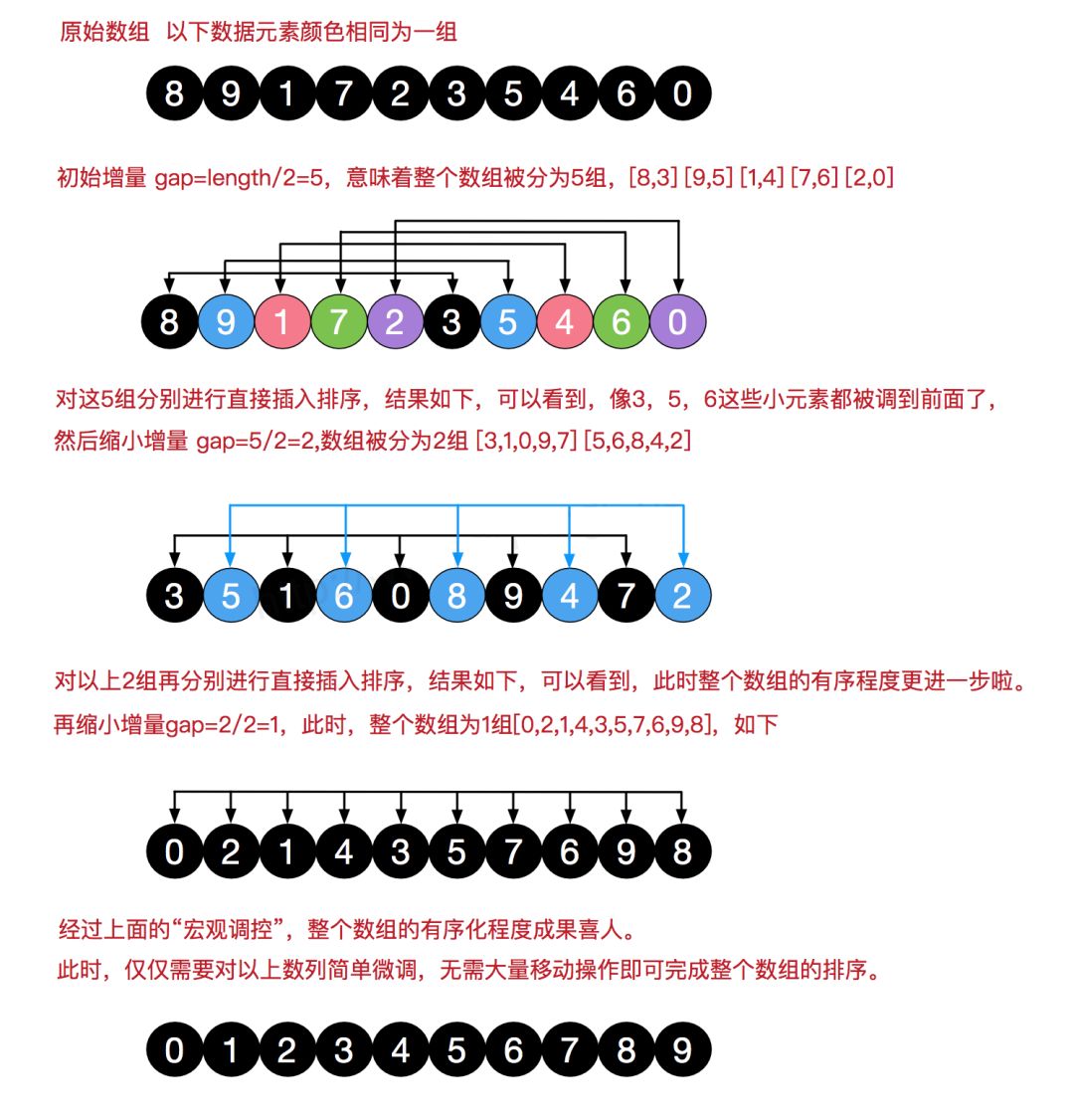
举例说明
这个算法无论怎么解释都会显得含糊不清,直接来个栗子,就拿上图来说明。
假设现在有一数组 arr: [8,9,1,7,2,3,5,4,6,0],我们设定初始化步长为 gap=arr.length/2=10/2,即 5。按照我们上面说的「跳跃分割策略」,按增量为 5 分割子数组,将每列看成是一个子数组:
|
|
// 列1 列2 列3 列4 列5 8 9 1 7 2 3 5 4 6 0 |
然后对每列进行类直接插入排序,可得:
|
|
// 列1 列2 列3 列4 列5 3 5 1 6 0 8 9 4 7 2 |
则此时原数组顺序应变成: [3,5,1,6,0,8,9,4,7,2],然后再缩小增量, gap=5/2=2,则数组分割如下:
|
|
// 列1 列2 3 5 1 6 0 8 9 4 7 2 |
继续对每列进行直接插入排序,可得:
|
|
// 列1 列2 0 2 1 4 3 5 7 6 9 8 |
则此时元素组顺序应变成: [0,2,1,4,3,5,7,6,9,8],这就是基本有序了。最后一轮再进行微调即可,所以此时增量应计算得为: gap=2/2=1,则直接对数组应用直接插入排序即可,最后得到:
|
|
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9] |
希尔排序具体实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
var shell_sort = function(arr){ var i, j, temp, gap; var len = arr.length; // 逐步缩小增量 for (gap=len>>1; gap>=1; gap>>=1) { // 类直接插入排序算法 for (i=gap; i<len; i++) { if (arr[i] < arr[i-gap]) { temp = arr[i]; for (j=i-gap; j>=0 && temp<arr[j]; j-=gap) { // 记录后裔,查找插入位置 arr[j gap] = arr[j]; } // 插入 arr[j gap] = temp; } } } return arr; }; shell_sort([8, 9, 1, 7, 2, 3, 5, 4, 6, 0]); |
不晓得大家有没有观察到,第一层循环里面的两层嵌套循环算法,其实就是「直接插入排序」,不同就在于多了一个变量 gap,但其实当 gap===1 时,那就跟我们上一节学到的算法,是完全一样的。
算法实现总结
通过以上代码的剖析,大家可以看到,希尔排序的关键不是简单地按 1 为增量进行分组排序后,再合并整体排序;而是选好一个初始化增量,不断地递减增量,每次递减之间都需要经过一次直接插入排序,使得排序的效率提高。
另外只要最终增量为 1,则任何增量序列都可以工作,因为最终当增量为 1 时,算法就变为「直接插入排序」,这就保证了数据一定会被排序。
复杂度分析
Donald Shell最初建议步长选择为 n/2 并且对步长取半直到步长达到1。虽然这样取可以比 O(n²) 类的算法(插入排序)更好,但这样仍然有减少平均时间和最差时间的余地。——维基百科
参考了一下维基百科及相关文章,获得如下结论:
- 希尔排序原始增量序列为 n/(2^i),也就是:n/2, n/4, ..., 1;最坏情况下时间复杂度为 O(n²)
- Hibbard 提出的增量序列为 2^k-1,也就是:1, 3, 7, ..., 2^k-1;最坏情况下时间复杂度为 O(n^(3/2))
- Sedgewick 提出的增量序列为已知的最好增量序列,也就是:1, 5, 19, 41, 109, .... ;该项序列的项来自
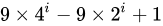 和
和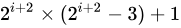
综上所述,希尔排序算法的出现,我们终于突破了慢速排序的时代,也即超越了时间复杂度为 O(n²)。
堆排序--文章结构
先上一张堆排序动画演示图片:
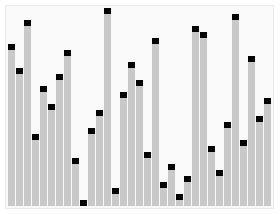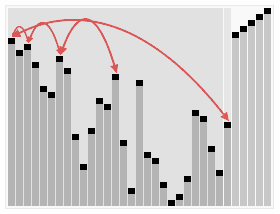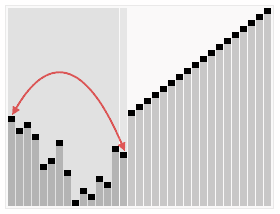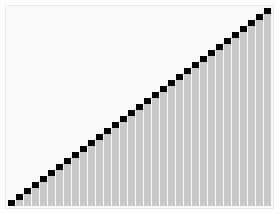
简单的二叉树
要了解堆,必须先了解一下二叉树,两者关系在下一步阐述。
二叉树(Binary Tree)是每一个节点最多有两个分支的树结构,通常分支被称作「左子树」和「右子树」,分支具有左右次序,不能随意颠倒。
二叉树第 i 层最多拥有 2^(i-1) 个节点,深度为 k 的二叉树最多共有 2^(k 1)-1 个节点,且定义根节点所在的层级 i=0,所在的深度 k=0。注意该定义在全文起作用,后续不继续提及。
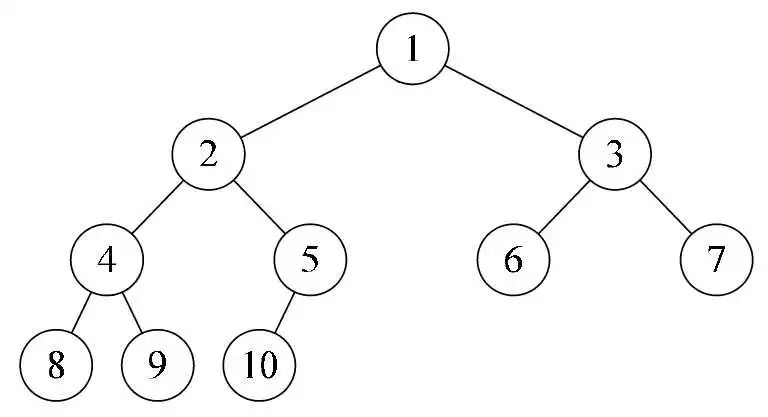
二叉树示意图
简单的满二叉树
假设某个二叉树深度为 k,第 i 层拥有 2^(i-1) 个节点,且总共拥有 2^(k 1)-1 个节点,这样的二叉树称为「满二叉树」。
换句话说,二叉树的每一层都是满的,除了最后一层上的节点,每一个节点都具有左节点和右节点。
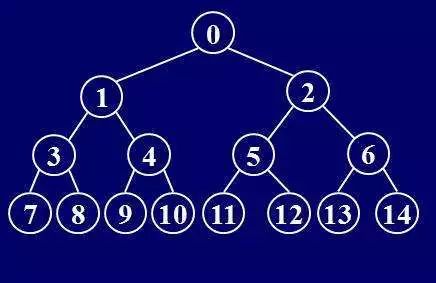
满二叉树示意图
简单的完全二叉树
假设某个二叉树深度为 k,共有 n 个节点,当且仅当其中的每一个节点,都可以和同样深度为 k 的满二叉树上的,按层序编号相同的节点,也就是序号为 1 到 n 的节点,均一一对应时,这样的二叉树称为「完全二叉树」。
满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树。
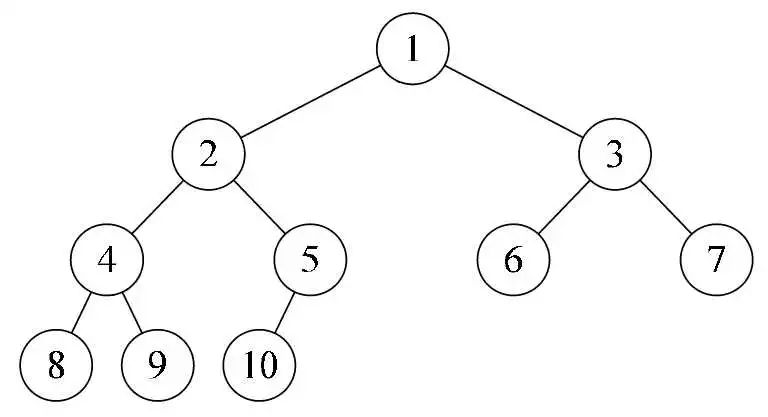
完全二叉树示意图
如下的就不是完全二叉树,树 1 中 10 号节点缺失,树 2 中 6、7 号节点缺失,树 3 中 10、11 号节点缺失。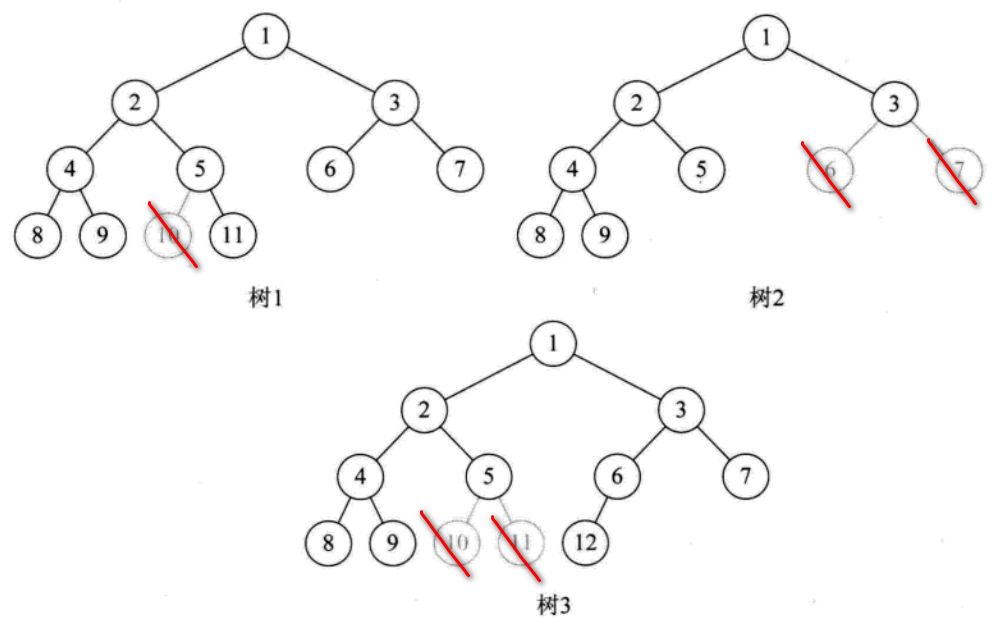
不是完全二叉树示意图
简单的堆
堆(Heap),一类特殊的数据结构的统称,通常是一个可以被看做一棵树的数组对象。
堆的实现通过构造二叉堆(binary heap),实为二叉树的一种,由于其应用的普遍性,当不加限定时,均指该数据结构的这种实现。
堆,是完全二叉树。

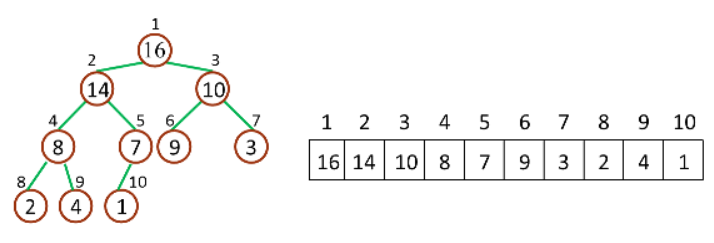
堆和数组相互关系示意图
对于给定的某个节点的下标 idx,可以很容易地计算出这个节点的父节点与孩子节点的下标:
|
|
// 计算父节点的下标 var getParentPos = function(idx){ return Math.floor(idx / 2); } // 计算左子节点的下标 var getLeftChildPos = function(idx){ return 2*idx; }; // 计算右子节点的下标 var getRightChildPos = function(idx){ return 2*idx 1; }; |
如下图,取下标 idx=4 的节点,则其父节点的下标就为 Math.floor(4/2)===2,其左子节点的下标就为 2*4===8,其右子节点的下标就为 2*4 1===9。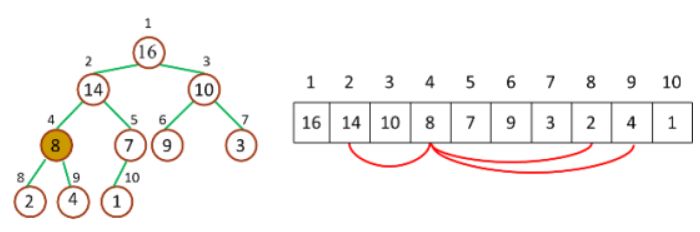
计算亲属节点位置示意图
但将堆转换为数组时,由于数组的初始化下标始终为 0,所以我们的堆数据结构模型在此时要发生如下改变: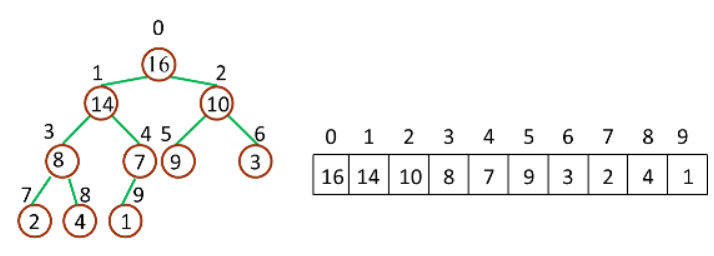
改变数据结构模型示意图
同样的,以上的算法也需要做一下微调:
|
|
// 计算父节点的下标 var getParentPos = function(idx){ return Math.floor((idx-1) / 2); } // 计算左子节点的下标 var getLeftChildPos = function(idx){ return 2*idx 1; }; // 计算右子节点的下标 var getRightChildPos = function(idx){ return 2 * (idx 1); }; |
简单的堆分类
二叉堆一般分为两种:「大顶堆」和「小顶堆」。
假设有一个堆,其中每个节点的值都大于或等于其左右孩子节点的值,则该堆称为「大顶堆」。「大顶堆」的最大元素值出现在根节点。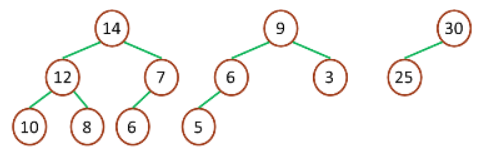
大顶堆示意图
假设有一个堆,其中每个节点的值都小于或等于其左右孩子节点的值,则该堆称为「小顶堆」。「小顶堆」的最小元素值出现在根节点。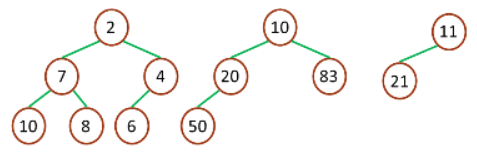
小顶堆示意图
算法介绍
堆排序,就是利用堆(假设利用大顶堆)进行排序的方法。
它的基本思想是,将待排序的数组构造成一个大顶堆。此时整个数组的最大值就是堆顶的根节点。将它移走,其实就是将其与堆数组的末尾元素交换,此时末尾元素就是最大值。然后将剩余的 n-1 个元素又重新构造成堆,这样就又能得到次大值。 如此反复操作,直到只剩余一个元素,就能得到一个有序数组了。
根据以上的算法指导,可理出如下关键操作:
- 大顶堆调整(Max-Heapify),将堆的末端子节点做调整,使得子节点永远小于父节点;
- 创建大顶堆(Build-Max-Heap),将堆中所有数据调整位置,使其成为大顶堆;
- 堆排序(Heap-Sort),移除在堆顶的根节点,并做大顶堆调整的迭代运算。
轻松实现大顶堆调整
大顶堆调整(Max-Heapify)的作用是保持大顶堆的性质,是创建大顶堆的核心子程序,一次作用过程如下图所示:
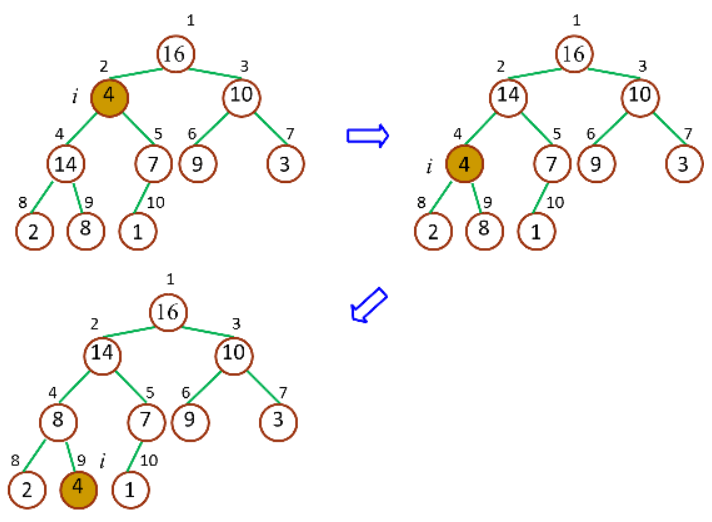
一次大顶堆调整示意图
由于一次调整后,仍有可能出现违反大顶堆的性质,所以需要递归地进行调整,直到整个堆都满足了条件。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
/** * 从 index 开始检查并保持大顶堆性质 * @arr 待排序数组 * @index 检查的起始下标 * @heapSize 堆大小 **/ var maxHeapify = function(arr, index, heapSize) { // 计算某节点与其左右子节点在位置上的关系 // 上一节讲过 var iMax = index, iLeft = 2 * index + 1, iRight = 2 * (index + 1); // 是否左子节点比当前节点的值更大 if (iLeft < heapSize && arr[index] < arr[iLeft]) { iMax = iLeft; } // 是否右子节点比当前更大节点的值更大 if (iRight < heapSize && arr[iMax] < arr[iRight]) { iMax = iRight; } // 如果三者中,当前节点值不是最大的 if (iMax != index) { swap(arr, iMax, index); maxHeapify(arr, iMax, heapSize); // 递归调整 } }; var swap = function(arr, i, j) { var temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }; |
上面代码将有个隐患,那就是当数组长度很大时,其中的递归函数有可能会引起内存爆栈。那我们不妨来用迭代来实现:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
var maxHeapify = function(arr, index, heapSize) { var iMax, iLeft, iRight; do { iMax = index; iLeft = 2 * index + 1; iRight = 2 * (index + 1); // 是否左子节点比当前节点的值更大 if (iLeft < heapSize && arr[index] < arr[iLeft]) { iMax = iLeft; } // 是否右子节点比当前更大节点的值更大 if (iRight < heapSize && arr[iMax] < arr[iRight]) { iMax = iRight; } // 如果三者中,当前节点值不是最大的 if (iMax != index) { swap(arr, iMax, index); index = iMax; } } while (iMax != index) } var swap = function(arr, i, j) { var temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } |
轻松实现创建大顶堆
创建大顶堆(Build-Max-Heap)的作用是,将一个数组改造成一个大顶堆,接受数组和堆大小两个参数,其中会自下而上地调用 Max-Heapify 来改造数组。
因为大顶堆调整(Max-Heapify)能够保证下标为 i 的节点之后的节点都满足大顶堆的性质,所以我们要自下而上地调用大顶堆调整(Max-Heapify)。
若最大顶堆的元素总数量为 n,则创建大顶堆(Build-Max-Heap)从下标为 getParentPos(n) 处开始,往上依次调用大顶堆调整(Max-Heapify)。过程如下图所示: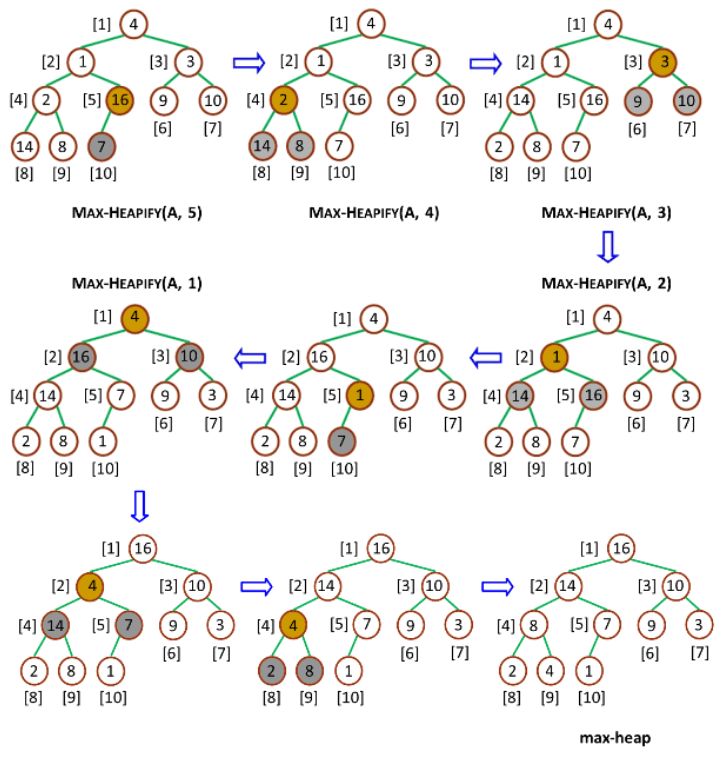
创建大顶堆过程示意图
算法实现如下:
|
|
var buildMaxHeap = function(arr, heapSize) { var i, iParent = Math.floor((heapSize - 1) / 2); for (i=iParent; i>=0; i--) { maxHeapify(arr, i, heapSize); } } |
轻松实现堆排序
堆排序(Heap-Sort)是堆排序的接口算法,其先要调用创建大顶堆(Build-Max-Heap)将数组改造为大顶堆;然后进入迭代,迭代中先将堆顶与堆底元素交换,并将堆长度缩短,继而重新调用大顶堆调整(Max-Heapify)保持大顶堆性质。
因为堆顶元素必然是堆中最大的元素,所以每一次操作之后,堆中存在的最大元素会被分离出堆,重复 n-1 次周,数组排序完成。过程如下图所示: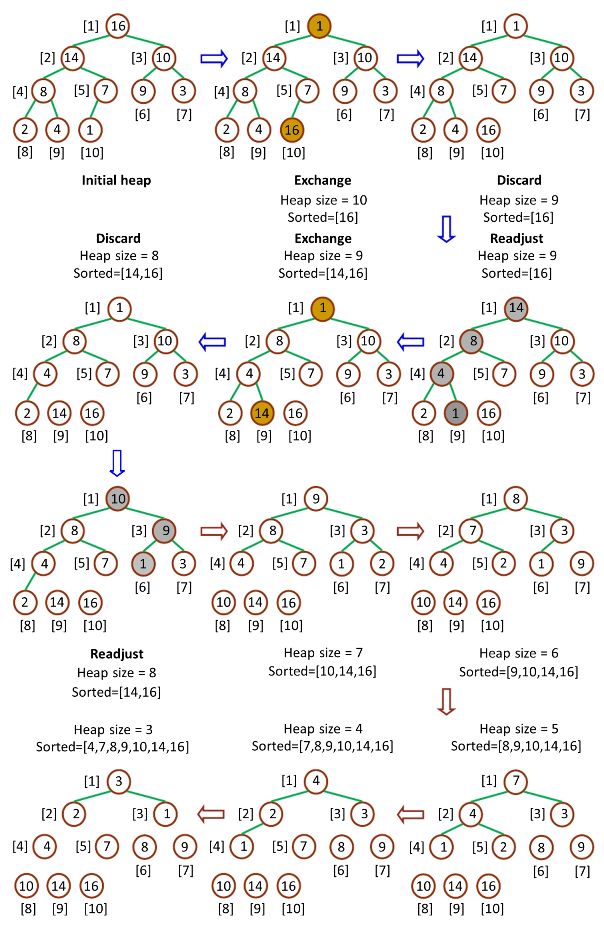
堆排序过程示意图
算法实现如下:
|
|
var heapSort = function(arr, heapSize){ var i; buildMaxHeap(arr, heapSize); for (i=heapSize-1; i>0; i--) { swap(arr, 0, i); maxHeapify(arr, 0, i); } }; |
完整实现
综合以上 3 块代码,完整的 js 代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
/* 大顶堆排序 */ var heapSort = function(arr, heapSize){ var i; buildMaxHeap(arr, heapSize); for (i=heapSize-1; i>0; i--) { swap(arr, 0, i); maxHeapify(arr, 0, i); } }; /* 创建大顶堆 */ var buildMaxHeap = function(arr, heapSize) { var i, iParent = Math.floor((heapSize - 1) / 2); for (i=iParent; i>=0; i--) { maxHeapify(arr, i, heapSize); } }; /* 大顶堆调整 */ var maxHeapify = function(arr, index, heapSize) { var iMax, iLeft, iRight; do { iMax = index; iLeft = 2 * index + 1; iRight = 2 * (index + 1); // 是否左子节点比当前节点的值更大 if (iLeft < heapSize && arr[index] < arr[iLeft]) { iMax = iLeft; } // 是否右子节点比当前更大节点的值更大 if (iRight < heapSize && arr[iMax] < arr[iRight]) { iMax = iRight; } // 如果三者中,当前节点值不是最大的 if (iMax != index) { swap(arr, iMax, index); index = iMax; } } while (iMax != index) } var swap = function(arr, i, j) { var temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } |
复杂度分析
堆排序的运行时间主要是消耗在初始构建堆和重建堆时的反复筛选上。
我们这里不深入探讨算法的时间复杂度计算,总体来说,堆排序的时间复杂度为 O(n*logn)。由于堆排序对原始数组的排序状态并不敏感,因此它无论最好、最坏还是平均时间复杂都为 O(n*logn)。这在性能上显然要优于冒泡、简单选择、直接插入等复杂度为 O(n^2) 的算法了。
另外,由于初始化构建堆所需的比较次数较多,因此它并不适合元素个数较少的数组。










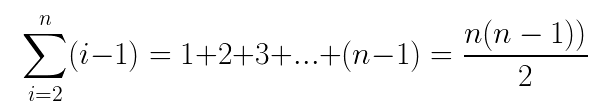
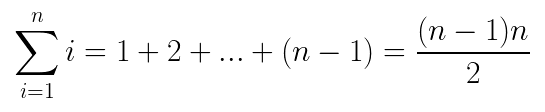

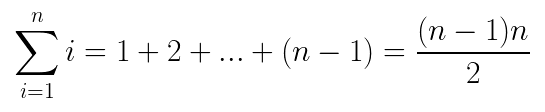
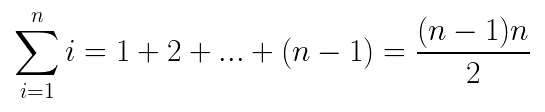
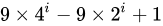 和
和